WHAT IS REGRESSION ANALYSIS?
Regression Analysis is a statistical method used to model the relationship between one or more independent variables (predictors) and a dependent variable (outcome). In hypothesis testing, regression analysis allows us to assess the significance of the relationships between these variables by testing specific hypotheses about the coefficients in the regression model.
TYPES OF REGRESSION
Simple Linear Regression
Models the relationship between a single independent variable X and dependent variable Y using a straight line.
Multiple Linear Regression
Extends simple linear regression to include multiple independent variables.
Nonlinear Regression
The relationship between the independent and dependent variables is nonlinear, involving nonlinear functions to model the data.
Polynomial Regression
Modeling the relationship between the independent and dependent variables using a polynomial equation of degree greater than one, allowing for curved relationships.
Logistic Regression
Dependent variable is categorical, typically binary (e.g., yes/no, pass/fail), to predict the probability of a particular outcome.
Ordinal Regression
Similar to logistic regression, but used when the dependent variable is ordinal (ranked categories) rather than binary.
Poisson Regression
Specifically designed for count data, where the dependent variable represents the number of occurrences of an event in a fixed interval of time or space.
Ridge Regression
A regularization technique used to mitigate multicollinearity in multiple regression models by adding a penalty term to the regression equation.
Lasso Regression
Another regularization technique that shrinks the coefficient estimates towards zero and performs variable selection by forcing some coefficients to be exactly zero.
Elastic Net Regression
Combines the penalties of ridge and lasso regression to address the limitations of each method and achieve a balance between bias and variance.
Quantile Regression
Estimates the conditional quantiles of the dependent variable, providing a comprehensive view of how different parts of the distribution respond to changes in the independent variables.
Bayesian Regression
Applies Bayesian statistics principles to regression analysis, incorporating prior knowledge and uncertainty into the estimation of regression parameters.
Time Series Regression
Analyzes time series data, where observations are collected sequentially over time, to model and forecast future values based on historical data.
RELATION TO HYPOTHESIS TESTING
TESTING REGRESSION MODELS
In hypothesis testing, we formulate null and alternative hypotheses regarding the coefficients in the regression model. For example, for the coefficient of an independent variable X the hypotheses can be stated as:
HYPOTHESIS FORMULAS
Null Hypothesis (H0) : β = 0 (no effect of X on Y)
Alternative Hypothesis (HA): β ≠ 0 (significant effect of X on Y)
TEST STATISTICS
To test the hypotheses, we calculate a test statistic based on the estimated coefficients from the regression model. Common test statistics include the t-statistic, F-statistic, or Wald statistic, depending on the specific hypothesis being tested.
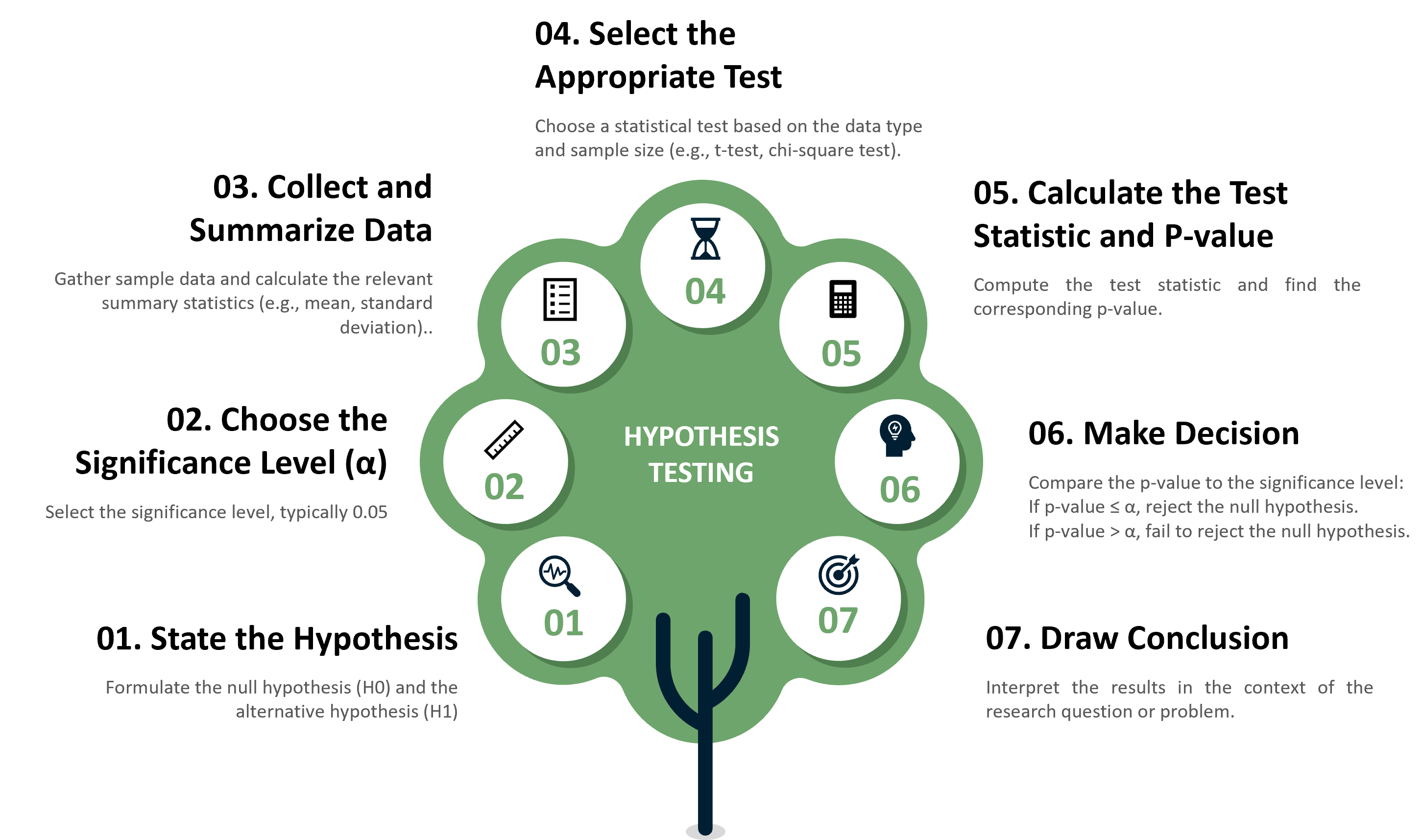
Steps in Conducting Hypothesis Testing